WAEC Mathematics Past Questions & Answers

Find the gradient of the line passing through the points $(\frac{1}{2}, \frac{- 1}{3}) and ( 3 , \frac{2}{3})$

$\frac{2}{5}$

$\frac{5}{2}$

$\frac{2}{7}$

$\frac{7}{2}$

View answer & explanation

Correct answer is A

Gradient(slope) m = $\frac{ y_2 - y_1}{ x_2 - x_1}$

the points are $(\frac{1}{2}, \frac{- 1}{3}) and ( 3 , \frac{2}{3})$

m = $\frac{\frac{2}{3} - (\frac{-1}{3})}{3 - \frac{1}{2}}$

= $\frac{\frac{2}{3} + \frac{1}{3}}{3 - \frac{1}{2}}$

= $1 \div\frac{5}{2}$ = $1\times\frac{2}{5}$

Therefore, m = $\frac{2}{5}$

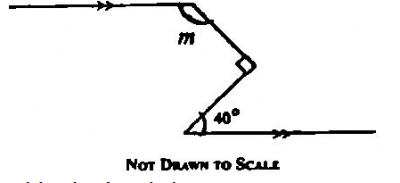
Find the value of m in the diagram above.

$40^0$

$50^0$

$130^0$

$140^0$

View answer & explanation

Correct answer is C

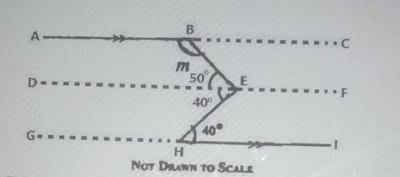
∠EHI = ∠DEH = 40° (alternate angles are equal)
∠BEH = 90° (given)
∠BED = 90° - 40° = 50°
∠BEF = 180° - 50° = 130° (sum of angles on a straight line is 180o)
∠BEF = ∠ABE = 130° (alternate angles are equal)
∴ m = 130°

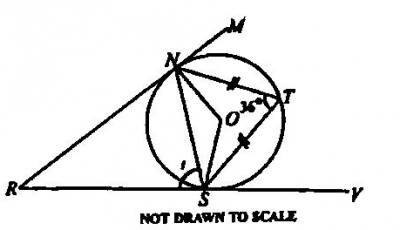
In the diagram above, O is the centre of a circle NST. |NT| = |ST| and ∠NTS = 36°. Find the measure of the angle marked t.

$72^0$

$54^0$

$36^0$

$108^0$

View answer & explanation

Correct answer is C

t = ∠NTS (the angle between a tangent and a chord is equal to the angle in the alternate segment).

Therefore, t = 36°

The length of the diagonal of a square is 12 cm. Calculate the area of the square.

$36 cm^2$

$48 cm^2$

$72 cm^2$

$18 cm^2$

View answer & explanation

Correct answer is C

Let each side be l, then area = $l^2$

Using Pythagoras theorem

$l^2 + l^2 = 12^2$

$2l^2 = 144$

divide both sides by 2

$l^2 = 72$

Therefore, the Area of the square is $72 cm^2$

10.

Find the quadratic equation whose roots are $\frac{2}{3} and \frac{- 3}{4}$

$12y^2 - y - 6 = 0$

$12y^2 - y + 6 = 0$

$12y^2 + y - 6 = 0$

$y^2 + y - 6 = 0$

View answer & explanation

Correct answer is C

Let p = $\frac{2}{3}$ and q = $\frac{- 3}{4}$

using (y - p)(y - q) = 0

= ( y - $\frac{2}{3})$ ( y - ( $\frac{- 3}{4})) = 0$

= ( $y - \frac{2}{3})( y + \frac{3}{4})$ = 0

$y^2 + \frac{3}{4}y - \frac{2}{3}y - \frac{6}{12} = 0$

$y^2 + \frac{1}{12}y - \frac{1}{2}$ = 0

= multiply through by the l. c. m of 3 and 4 = 12

∴ the quadratic equation is $12y^2 + y - 6 = 0$

First
1
2
3
4
5
6
7
8
9

WAEC Subjects

Literature in English

Islamic Religious Knowledge

Christian Religious Knowledge

Aptitude Tests

Spatial Reasoning Questions and Answers

Microsoft Office Questions and Answers

Nigeria General Knowledge Questions and Answers

Verbal Reasoning Questions and Answers

Situational Judgement Questions and Answers

Abstract Reasoning Questions and Answers

Data Interpretation Questions and Answers

Logical Reasoning Questions and Answers

Typing Speed and Accuracy Test

Numerical Reasoning Questions and Answers

Puzzles Questions and Answers

Quantitative Reasoning Questions and Answers

Personality Test

See all →

View latest jobs in Nigeria today

WAEC Mathematics Past Questions & Answers - Page 2

WAEC Subjects

Aptitude Tests