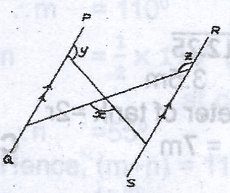
In the diagram, PQ//RS. Find x in terms of y and z
x = 240\(^o\) - y - z
x = 180\(^o\) - y - z
x = 360\(^o\) + y -z
x = 360\(^o\) - y - z
Correct answer is D
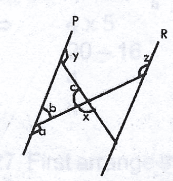
In the diagram,
a = z (alternate angles)
b = 180\(^o\) - a (angles on a straight line)
b = 180\(^o\) - z
c = 180\(^o\) - x (angles on a straight line)
y = b + c (sum of oposite interior angles)
y = 180\(^o\) - z + 180\(^o\) - x
y = 360\(^o\) - z - x
x = 360\(^o\) - y - z
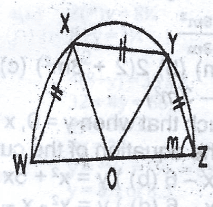
90\(^o\)
60\(^o\)
45\(^o\)
30\(^o\)
Correct answer is B
In the diagram, < WOZ = 180\(^o\) (angle on a straight line)
< WOX = < XOY = < YOZ
(|WX| = |XY| = |YZ|)
\(\frac{180^o}{3}\) = 60\(^o\)
= 60\(^o\)
M + m =2m (base angles of isosceles \(\bigtriangleup\), |OY| and |OZ| are radii)
< YOZ + 2m (base angles of a \(\bigtriangleup\))
60\(^o\) + 2m = 180\(^o\) (sum of a \(\bigtriangleup\))
60\(^o\) + 2m = 180\(^o\)
2m = 180\(^o\) - 60\(^o\)
2m = 120\(^o\)
m = \(\frac{120^o}{2}\)
= 60\(^o\)

The solution of x + 2 \(\geq\) 2x + 1 is illustrated
i
ii
iii
iv
Correct answer is A
x + 2 \(\geq\) 2x + 1
x - 2x \(\geq\) 1 - 2
-x \(\geq\) -1
\(\frac{-x}{-1}\) \(\geq\) \(\frac{-1}{-1}\)
x \(\leq\) 1
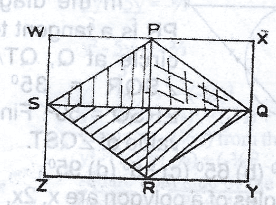
25cm\(^2\)
24cm\(^2\)
16cm\(^2\)
12cm\(^2\)
Correct answer is B
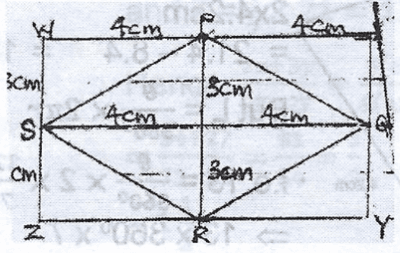
Area of shaded part = 2 x area of \(\bigtriangleup\)SPQ
= 2 x \(\frac{1}{2}\) 8 x 3 =24cm
Hence, area of the unshaded part of the rectangle = area of rectangle - area of shaded part
= 8 x 6 - 24
= 48 - 24
= 24 cm\(^2\)
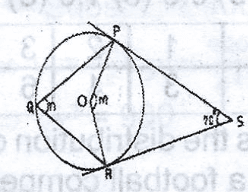
110\(^o\)
135\(^o\)
165\(^o\)
225\(^o\)
Correct answer is C
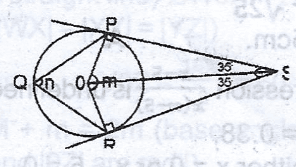
In the diagram,
Thus, m = 2 x 55\(^o\) (is a bisector of obtuse
m = 110\(^o\)
n = \(\frac{1}{2}\) x 110\(^o\) (angle at centre = 2 x angle at circum)
n = 55\(^o\)
m + n = 110 + 55 = 165\(^o\)
WAEC Subjects
Aptitude Tests