Given that Y is 20cm on a bearing of 300\(^o\) from x, how far south of y is x?
10cm
15cm
25cm
30cm
Correct answer is A
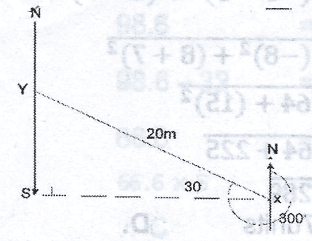
In \(\bigtriangleup\)YSC, sin 30\(^o\) = \(\frac{YS}{20}\)
|YS| = 20 sin 30\(^o\)
= 20 x 0.5
10m
If tan x = \(\frac{4}{3}\), 0\(^o\) < x < 90\(^o\), find the value of sin x - cos x
\(\frac{1}{10}\)
\(\frac{1}{5}\)
\(\frac{5}{12}\)
1\(\frac{2}{5}\)
Correct answer is B
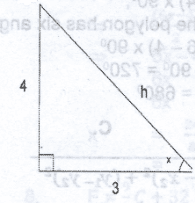
From the diagram,
h\(^2\) = 4\(^2\) + 3\(^2\) (pythagoras')
h\(^2\) = 16 + 9 = 25
h = \(\sqrt{25}\) = 5
Hence, sin x - cos x
= \(\frac{4}{5} - \frac{3}{5}\)
= \(\frac{1}{5}\)
170\(^o\)
192\(^o\)
177\(^o\)
182\(^o\)
Correct answer is B
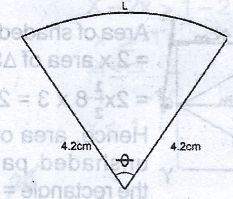
Length of arc, L = 21.4 - 2 x 4.2cm
= 21.4 - 8.4
= 13cm
But L = \(\frac{\theta}{360^o}\) x 2\(\pi r\)
i.e 13 = \(\frac{\theta}{360^o}\) x 2 x \(\frac{22}{7}\) x 4.2
= 13 x 360\(^o\) x 7
= \(\theta\) x 2 x 22 x 4.2
\(\theta\) = \(\frac{13 \times 360^o \times 7}{44 \times 4.2}\)
= \(\approx\) 177.27\(^o\)
\(\approx\) 177\(^o\) (to the nearest degree)

N26,792.00
N26,972.00
N62.792.00
N62,972.00
Correct answer is D
Total donation = 4 x 500 + 7 x 2000 + 20 x 1000 + 9 x 700 + 4 x 500 + 5 x 100 + 3 x 50 + 1 x 2 + 2 x 10 = 20000 + 14000 + 20000 + 6300 + 2000 + 500 + 150 + 2 + 20 = N62,972
2 : 3 : 4
3 : 4 : 5
4 : 5 : 6
5 : 6 : 7
Correct answer is D
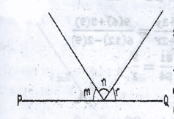
m + n = 110\(^o\), (n + r) = 130\(^o\)
(m + n) = 120\(^o\)
then, r = 130\(^o\) - n
and;
m + (130^o - n) = 120\(^o\)
m - n = -10\(^o\)
2m + (n + r) = 110 + 120 = 230
2m + 130 = 230
2m = 230 - 130
m = \(\frac{100}{2}\) = 50\(^o\)
n = 110\(^o\) - 50\(^o\)
= 60\(^o\)
r = 130\(^o\) - 60\(^o\) = 70\(^o\)
Hence, the ratio m : n : r
= 50 : 60 : 70
= 5 : 6 : 7
WAEC Subjects
Aptitude Tests