If x varies inversely as y and y varies directly as z, what is the relationship between x and z?
x \(\alpha\) z
x \(\alpha\) \(\frac{1}{z}\)
a \(\alpha\) z\(^2\)
x \(\alpha\) \(\frac{1}{z^2}\)
Correct answer is B
\(x \propto \frac{1}{y}\), y \(\propto\) z
x = \(\frac{k}{y}\)
y = mz
Since y = mz,
x = \(\frac{k}{mz}\), where k and m are constants. Hence,
x \(\propto\) \(\frac{1}{z}\)
Express 0.0000407, correct to 2 significant figures
0.0
0.00004
0.000041
0.0000407
Correct answer is C
0.0000407 to 2 s.f 0.000041 (2 s.f)
The graph of y = x\(^2\) and y = x intersect at which of these points?
(0,0), (1,1)
(0,0), (0,1)
(1, 0), (0, 0)
(0, 0) (0, 0)
Correct answer is A
y = x\(^2\) ....(1)
y = x ......(2)
y = y
x\(^2\) - x
x\(^2\) - x = 0
x(x - 1) = 0
x = 0 or x - 1 = 0
x = 0 or x = 1
when x = 0, y = 0\(^2\) = 0
when x = 1, y = 1\(^2\) = 1
Hence; the two graphs interest at (0, 0) and (1, 1)
18
20
30
38
Correct answer is D
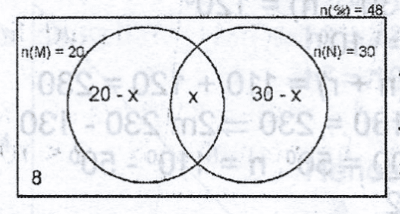
Let n(M \(\cup\) N \) = x
Then 20 - x + x + 30
- x = n(M \(\cup\) N)
50 - x = 40
50 - 40 = x
10 = x
x = 10
Hence, n(M \(\cup\N)' = 8 + (20 - 10) + (30 + 10)
= 8 + 10 + 20
= 38
42cm
48cm
52cm
60cm
Correct answer is C
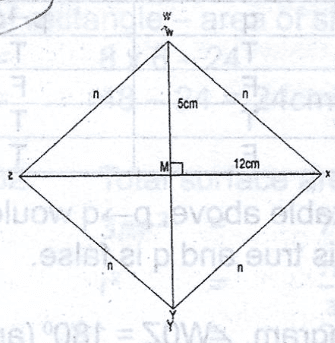
Let the length of a side of the rhombus be n
Then, n\(^2\) = 5\(^2\) + 12\(^2\)
= 25 + 144 = 169
n = \(\sqrt{169}\)
= 13cm
Hence, perimeter of rhombus = 4n = 4 x 13
= 52cm
WAEC Subjects
Aptitude Tests