Simplify:(\(\frac{10\sqrt{3}}{\sqrt{5}} - \sqrt{15}\))2
75.00
15.00
8.66
3.87
Correct answer is B
Note that \(\frac{10\sqrt{3}}{\sqrt{5}} = \frac{10\sqrt{3}}{\sqrt{5}} \times - \frac{\sqrt{5}}{\sqrt{5}}\)
= \(\frac{10\sqrt{15}}{\sqrt{5}} = 2\sqrt{15}\)
hence, (\(\frac{10\sqrt{3}}{\sqrt{5}} - \sqrt{15}\))2 = (\(2\sqrt{15} - \sqrt{15}\))2
= (\(2\sqrt{15} - \sqrt{15}\))(\(2\sqrt{15} - \sqrt{15}\))
= 4\(\sqrt{15 \times 15} - 2\sqrt{15 \times 15} - 2\sqrt{15 x 15} + \sqrt{15 \times 15}\)
= 4 x 15 - 2 x 15 - 2 x 15 + 15
= 60 - 30 - 30 + 15
= 15
Simplify: (\(\frac{3}{4} - \frac{2}{3}\)) x 1\(\frac{1}{5}\)
\(\frac{1}{60}\)
\(\frac{5}{72}\)
\(\frac{1}{10}\)
1\(\frac{7}{10}\)
Correct answer is C
(\(\frac{3}{4} - \frac{2}{3}\)) x 1\(\frac{1}{5}\)
= (\(\frac{9 - 8}{12} \times \frac{6}{5}\))
= \(\frac{1}{12} \times \frac{6}{5}\)
= \(\frac{1}{10}\)
If 23x + 101x = 130x, find the value of x
7
6
5
4
Correct answer is D
23x + 101x = 130x
2 x X1 + 3 x Xo + 1 x X2 + 0 x X1 + 1 x Xo
= 1 x Xo = 1 x X2 + 3 x X1 + 0 x Xo
= X2 + 3x + 0
2x + 3 = x2 + 0 + 1 + x2 + 3x
2x - 3x + x2 - x2 = -3 - 1
- x = -4
x = 4
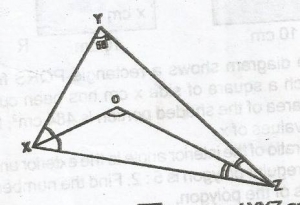
68o
72o
112o
124o
Correct answer is D
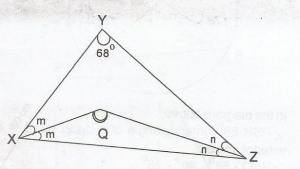
In \(\Delta\) XYZ, 2m + 2n + 68o = 180o
2(m + n) + 68o = 180o...(1)
in \(\Delta\) XOZ, m + n + q = 180o ...(2)
(m + n) = 180o - q...(3)
substituting 180o - q for (m + n) in (1) gives
2(180o - q) + 68o = 180o
360o - 2q = 180o - 68o
360o - 2q = 112o
360o - 112o = 2q
248o = 2q
q = \(\frac{248^o}{2}\)
= 124o
hence, < XOZ = 124o
22cm
17cm
16cm
15cm
Correct answer is B
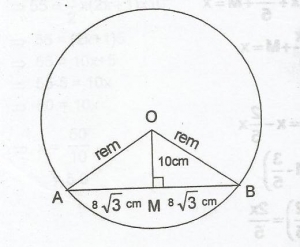
In the diagram
|AM| = |MB| - \(\frac{|AB|}{2}\)
= \(\frac{16\sqrt{3}}{2}\)cm
= 8\(\sqrt{3}\)cm
in \(\Delta\) AMO, r2 = |AM|Z + |MO|2
r2 = (8\(\sqrt{3}\))2
+ 102
= 64 x 3 + 100
= 192 + 100
= 292
r = \(\sqrt{292}\)
17.088cm
17cm
WAEC Subjects
Aptitude Tests