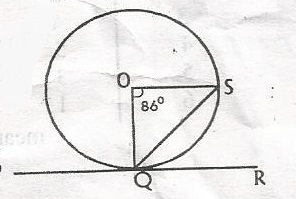
43o
47o
54o
86o
Correct answer is A
Construction: draw a line from Q to point P and another line from S to point P.
< SOQ = 2< QPS (< at centre is twice < on the circumference)
< QPS \(\frac{86}{2} = 43\)
< SQR = < QPS ( < between a chord and tangent = < in the alternate segment)
< SQR = 43o
In which of the following situations is friction not useful?
Operation of a grinding machine
Walking
Application of brakes
Moving piston in a sleeve
Correct answer is D
friction, force that resists the sliding or rolling of one solid object over another.
Examples of friction in our daily life
- Driving of a a vehicle on a surface.
- Applying brakes to stop a moving vehicle.
- Skating.
- Walking on the road.
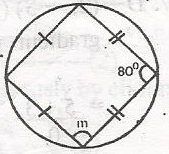
Determine the value of m in the diagram
80o
90o
110o
150o
Correct answer is B
No explanation has been provided for this answer.
The basic principle of operation of a beam balance is-----------------
Hooke's law
Archimedes principle
law of flotation
principle of moments
Correct answer is D
Hooke's Law states that the extension of a spring is proportional to the load that is applied to it. A variety of materials obey this law as long as the load does not exceed the material's elastic limit.
Archimede's Principle states that a body immersed in a fluid experiences an upthrust equal to the weight of the fluid displaced, and this is fundamental to the equilibrium of a body floating in still water.
When a body floats in a liquid, the weight of the liquid displaced by its immersed part is equal to the total weight of the body. This is the law of floatation.
The Principle of Moments states that when a body is balanced, the total clockwise moment about a point equals the total anticlockwise moment about the same point.
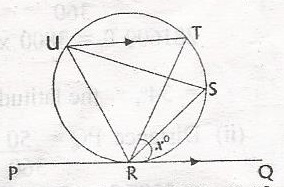
2xo
(90 - x)o
(90 + x)o
(180 - 2x)o
Correct answer is D
< URT = < TRQ (angle alternate a tangent and a chord equal to angle in the alternate segment)
< RUT = xo
In \(\bigtriangleup\) URT
< RUT + < RUT + < UTR = 180o (sum of int. < s of \(\bigtriangleup\))
< URT + x + x = 180o
< URT = 180o - 2x
WAEC Subjects
Aptitude Tests