Mathematics Questions and Answers

The two trailing zeros in the number are not significant, but the other five are, making it a five-figure number.

|AP| = |PB| = $x$ (The perpendicular to a chord bisects the chord if drawn from the center of the circle.)

From ∆OPB

Using Pythagoras theorem

⇒ $13^2 = 12^2 + x^2$

⇒ $169 = 144 + x^2$

⇒ $169 - 144 = x^2$

⇒ $x^2 = 25$

⇒ $x = \sqrt25 = 5 cm$

∴ Length of the chord |AB| = $x  + x  = 5 + 5 = 10 cm$

On the $y$-axis, each box is $\frac{1 - 0}{5} = \frac{1}{5}$ = 0.2unit

On the $x$-axis, each box is $\frac{90 - 0}{6} = \frac{90}{6} = 15^o$

⇒ $θ_1 = 180^o + (2.5\times15^o) = 180^o + 37.5^o = 217.5^o ≃ 218^o$(2 and half boxes were counted to the right of 180$^o$)

⇒ $θ_2 = 270^o + (3.5\times15^o) = 270^o + 52.5^o = 322.5^o ≃ 323^o$(3 and half boxes were counted to the right of 270$^o$)

∴ $θ = 218^o, 323^o$

AB = $\frac{θ}{360}\times 2\pi Rcos\propto$ (distance on small circle)

= 64 - 56 = 8$^o$

$\propto = 86^o$

⇒ AB = $\frac{8}{360}$ x 2 x 3.142 x 6370 x cos 86

⇒ AB = $\frac{22,338.29974}{360}$

∴ AB = 62km (to the nearest km)

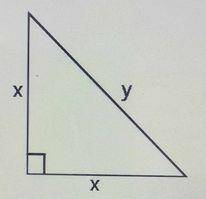
Perimeter of a triangle = sum of all sides

⇒ $P = y + x + x = 2$

⇒ $y + 2x = 2$

⇒ $y= 2 - 2x$-----(i)

Using Pythagoras theorem

$y^2 = x^2 + x^2$

⇒ $y^2 = 2x^2$

⇒ $y = \sqrt2x^2$

⇒ $y = x\sqrt2$-----(ii)

Equate $y$

⇒ $2 - 2x = x\sqrt2$

Square both sides

⇒ $(2 -2x) ^2 = (x\sqrt2)^2$

⇒ $4 - 8x + 4x^2 = 2x^2$

⇒ $4 - 8x + 4x^2 - 2x^2 = 0$

⇒ $2x^2 - 8x + 4 = 0$

⇒ $x = \frac{-(-8)\pm\sqrt(-8)^2 - 4\times2\times4}{2\times2}$

⇒ $x = \frac{8\pm\sqrt32}{4}$

⇒ $x = \frac{8\pm4\sqrt2}{4}$

⇒ $x = 2\pm\sqrt2$

⇒ $x = 2 + \sqrt2$ or $2 - \sqrt2$

∴ $x = 2 - \sqrt2$ (for $x$ has to be less than its perimeter)

∴ $y = 2 - 2x = 2 - 2(2 - \sqrt2) = -2 + 2 \sqrt2$

∴ The length of the longer side = -2 + 2$\sqrt2$m