Mathematics Questions and Answers

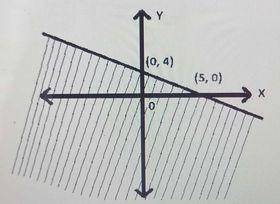
First, we find the equation of the boundary line using the two intercepts.The slope is

m = \(\frac{4 - 0}{0 - 5} = {4}{5}\)

The y-intercept is 4

The slope-intercept form of the equation is therefore

y = -\(\frac{4}{5} x + 4\)

\(\implies y + \frac{4}{5} x = 4\)

Multiply both sides by \(\frac{5}{4}\)

\(\implies\frac{5}{4}(y +\frac{4}{5} x) = 4\times\frac{5}{4}\)

\(\implies\frac{5}{4} y + x = 5\)

Multiply both sides by 4

⇒ \(5y + 4x = 20\)

The inequality is therefore either \(5y + 4x ≤ 20\) or \(5y + 4x ≥ 20.\)

Using the test point (0, 0) -The origin

⇒ 5(0) + 4(0) ≤ 20

⇒ 0 ≤ 20 (True)

∴ The inequality is \(5y + 4x ≤ 20\)

Intersecting Chords Theorem states that If two chords intersect in a circle, then the products of the measures of the segments of the chords are equal.

⇒ AE * EB = CE * ED

⇒ 6 * \(x\) = 4 * (\(x\) + 5)

⇒ 6\(x\) = 4\(x\) + 20

⇒ 6\(x\) - 4\(x\) = 20

⇒ 2\(x\) = 20

∴ \(x = \frac{20}{2}\) = 10 units

Area of the composite figure = Area of semi circle + Area of rectangle + Area of triangle

Area of semi circle = \(\frac{1}{2}\pi r^2 = \frac{1}{2}\times\pi\times\frac{d^2}{4} = \frac{1}{2}\times\frac{22}{7}\times\frac{42^2}{4} = 693 m^2\)

Area of rectangle = l x b = 42 x 60  =2520 m\(^2\)

Area of triangle = \(\frac{1}{2}\times b \times h = \frac{1}{2}\times 36 \times 42 = 756 m^2\)

∴ Area of the composite figure = 693 + 2520 + 756 = 3969 m\(^2\)

\(log_2 (6 - x) = 3 - log_2 x\)

⇒ \(log_2 (6 - x) = 3 log_2 2 - log_2 x\) (since \(log_2\) 2 = 1)

⇒ \(log_2 (6 - x) = log_2 2^3 - log_2 x\) \((a log\) c = \(log\) c\(^a)\)

⇒ \(log_2 (6 - x) = log_2 8 - log_2 x\)

⇒\(log_2 (6 - x) = log_2 \frac{8}{x}\) (\(log\) a - \(log\) b = \(log \frac{a}{b})\)

⇒ \(6 - x = \frac{8}{x}\)

⇒ \(x (6 - x) = 8\)

⇒ \(6x - x^2 = 8\)

⇒ \(x^2 - 6x + 8 = 0\)

⇒ \(x^2 - 4x - 2x + 8 = 0\)

⇒ \(x (x - 4) - 2(x - 4) = 0\)

⇒ \((x - 4)(x - 2) = 0\)

⇒ \(x - 4 = 0 or x - 2 = 0\)

∴ x = 4 or 2

Let number of children's ticket at ₦250.00 each = \(x\)

∴ Number of adult tickets at ₦520.00 each = 5\(x\)

Then,

Total amount of money received from children's tickets = 250\(x\)

Total amount of money received from adult tickets = 520(5\(x\))

⇒ 250\(x\) + 520(5\(x\)) = 171,000

⇒ 250\(x\) + 2600\(x\) = 171,000

⇒ 2850\(x\) = 171,000

⇒ \(x = \frac{171,000}{2850} = 60\)

∴ 60 tickets were sold at ₦250.00 and 300 tickets were sold at ₦520.00