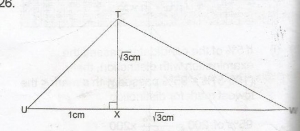
WAEC Past Questions and Answers - Page 2666

13,326.

In the diagram, TX is perpendicular to UW, |UX| = 1cm and |TX| = |WX| = \(\sqrt{3}\)cm. Find UTW

135^o

105^o

75^o

60^o

View answer & explanation

Correct answer is C

In \(\Delta\) UXT, tan\(\alpha\) = \(\frac{1}{\sqrt{3}}\)

\(\alpha\) = tan^-1(\(\frac{1}{\sqrt{3}}\))

= 30^o

In \(\Delta\)WXT, tan\(\beta\) \(\frac{\sqrt{3}}{\sqrt{3}}\) = 1

\(\beta\) = tan^-1(1) = 45^o

Hence, < UTW = \(\alpha\) + \(\beta\)

= 30^o + 45^o = 75^o

13,327.

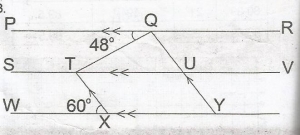
In the diagram, PR||SV||WY|, TX||QY|, < PQT = 48^o and < TXW = 60^o.Find < TQU.

120^o

108^o

72^o

60^o

View answer & explanation

Correct answer is C

In the diagram, < TUQ + 60^o(corresp. angles)

< QTU = 48^o (alternate angles)

< QU + 60^o + 48^o = 180^o(sum of angles of a \(\Delta\))

< TQU = 180^o - 108^o

= 72^o

13,328.

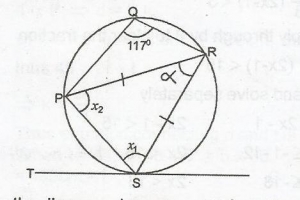
In the diagram, TS is a tangent to the circle at S. |PR| and < PQR = 177^o. Calculate < PST.

54^o

44^o

34^o

27^o

View answer & explanation

Correct answer is A

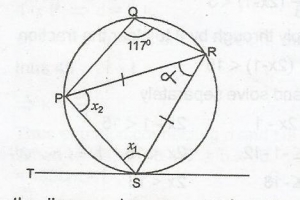
In the diagram above, x₁ = 180^o - 117^o = 63^o(opposite angles of a cyclic quad.)

x₁ = x₂ (base angles of isos. \(\Delta\))

x₁ + x₂ + \(\alpha\) = 180^o (sum of angles of a \(\Delta\)

63^o + 63^o + \(\alpha\) = 180^o

\(\alpha\) = 180^o - (63 + 63)^o

= 54^o

13,329.

Kweku walked 8m up to slope and was 3m above the ground. If he walks 12m further up the slope, how far above the ground will he be?

4.5m

6.0m

7.5m

9.0m

View answer & explanation

Correct answer is C

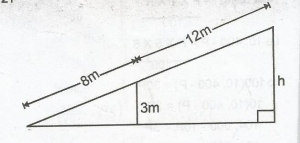
By similar triangles, \(\frac{8}{3}\) = \(\frac{8 + 12}{h}\)

\(\frac{8}{3} = \frac{20}{h}\)

h = \(\frac{3 \times 20}{8}\)

= 7.5m

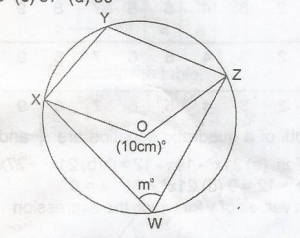
13,330.

In the diagram, O is the centre of the circle, < XOZ = (10cm)^o and < XWZ = m^o. Calculate the value of m.

View answer & explanation

Correct answer is A

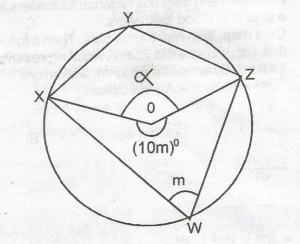
In the diagram above, \(\alpha\) = 2m^o (angle at centre = 2 x angle at circumference)

\(\alpha\) + 10m^o = 360^o (angle at circumference)

\(\alpha\) + 10m^o = 360^o(angles round a point)

2m^o + 10m^o = 360^o

12m^o = 360^o

m^o = \(\frac{360^o}{12}\)

= 30^o