2.0
3.0
2.5
4.0
Correct answer is C
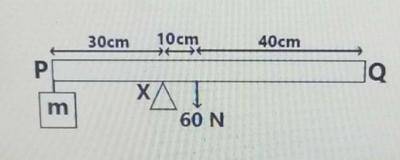
∑ clock wise moments =∑ anti clock wise moments
= 60 x 10 = 30 x m
= 600 = 30 m
m = \(\frac{600}{30} = 20 N\)
W = mg ==> m = \(\frac{W}{g}\)
∴ m = \(\frac{20}{10} = 2kg\)
If \(f : x → 2 tan x\) and \(g : x → √(x^2 + 8), find ( g o f )(45^o)\)
4
2√3
6
3√2
Correct answer is B
\(f : x → 2 tan x\)
\(g : x → √(x^2 + 8)\)
\(( g o f ) = √((2 tan x)^2 + 8)\)
\(( g o f )(45º) = √((2 tan 45º)^2 + 8)\)
= √(4 + 8) = √12
= √(4 x 3)
∴ 2√3
\(8\sqrt2^n\)
\(2^{(n+2)}\sqrt2\)
\(\sqrt2^{(n+3)}\)
\(8n\sqrt2\)
Correct answer is B
8√2, 16√2, 32√2, ..
\(a = 8\sqrt2; r =\frac{T_2}{T_1}=\frac{16\sqrt2}{8\sqrt2}=2\)
\(T_n=ar^{n-1}\)
\(T_n=8\sqrt2 \times 2^{n-1}\)
\(T_n=2^3\times2^{n-1}\times\sqrt2\)
\(T_n=2^{3+n-1}\times\sqrt2\)
\(\therefore T_n= 2^{(n+2)}\sqrt2\)
Solve 6 sin 2θ tan θ = 4, where 0º < θ < 90º
18.43º
30.00º
35.26º
19.47º
Correct answer is C
6 sin 2θ tan θ = 4, where 0º < θ < 90º
sin 2θ = 2sin θ cos θ and tanθ = \(\frac{sinθ}{cosθ}\)
= 6 x 2sin θ cos θ x \(\frac{sin θ}{cos θ} = 4\)
= \(sin^2 θ = 4\)
= \(sin^2 θ = \frac{4}{12}=\frac{1}{3}\)
=\(sin θ = \frac{\sqrt1}{3}=\frac{1}{\sqrt3}\)
= \(θ = sin^{-1}(\frac{1}{\sqrt3})\)
∴ θ = 35.26º
Given that r = (10 N , 200º) and n = (16 N , 020º), find (3r - 2n).
(62 N , 240º)
(62 N , 200º)
(62 N , 280º)
(62 N , 020º)
Correct answer is D
r = (10 N, 200º) and n = (16 N, 020º)
In rectangular form:
r = 10cos 200ºi + 10sin 200ºj = -9.397i - 3.420j
n = 16cos 20ºi + 16sin 20ºj = 15.035i + 5.472j
3r = -28.191i - 10.260j
2n = 30.070i + 10.945j
3r - 2n = (-28.191i - 10.260j) - (30.070i + 10.945j)
3r - 2n = -58.261i - 21.205j
|3r - 2n| = √((-58.261)\(^2\) + (-21.205)\(^2\)) = 62 N
\(tan θ =\frac{-21.205}{-58.261} = 0.3640\)
\(θ = tan^{-1} (0.3640) = 20^o\)
∴ (62 N , 020º)
WAEC Subjects
Aptitude Tests